Setting Up Infobox Templates in MediaWiki

Note: This guide has been updated as of 2014-09-22 for MediaWiki v1.23. If you’re using this version (or later) please see the Infoboxes in MediaWiki v1.23 post.

** Click here for the updated post. **

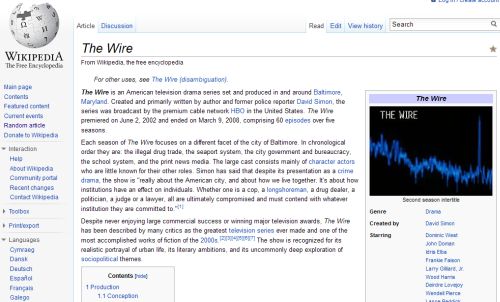
If you’ve ever been to any of the more structured Wikipedia pages you probably have seen the neat “infoboxes” that they have on the right hand side. They’re a neat, convenient way to get some of the core metainfo from an article.

If you have your own MediaWiki instance, you’ve probably thought they’d be a nice thing to have, so maybe you copy and pasted the code from Wikipedia and then were surprised when it didn’t just magically work. Turns out that the infobox stuff is part of MediaWiki’s extensive Templating system, so first of all you need the templates. Sounds easy, right?

Well, no. You don’t just flip a switch or download a file, and when you do a search you might find this article which details a process that it says might take 60-90 minutes.

I started looking into it and quickly got lost; you basically need to create a billion different Templates and do all sorts of weird stuff to get it to work. Fortunately I stumbled across this discussion which contained a clue that greatly simplifies the process.

I was able to distill the steps down to a process that I was able to reproduce on a new MediaWiki install in about five minutes. Before we start, I’ll throw in the warning that I have not read the documentation and I don’t understand at a low level what is happening with the templating. I just wanted a working, simple infobox.

  1. Download the MediaWiki extension ParserFunctions and add it to your LocalSettings.php as referred to there.
  2. Copy the CSS required to support the infobox from Wikipedia to your Wiki. The CSS is available in Common.css. You’ll probably need to create the stylesheet – it will be at http://your_wiki/wiki/index.php?title=MediaWiki:Common.css&action=edit – and then you can just copy/paste the contents in there. (I copied the whole file; you can probably just copy the infobox parts.)
  3. Export the infobox Template from Wikipedia:
    1. Go to Wikipedia’s Special:Export page
    2. Leave the field for ‘Add pages from category’ empty
    3. In the big text area field, just put in “Template:Infobox”.
    4. Make sure the three options – “Include only the current revision, not the full history”, “Include templates”, and “Save as file” – are all checked
    5. Hit the ‘Export’ button; it will think for a second then spit out an XML file containing all the Wikipedia Templates for the infobox for you to save to your PC.
  4. Now you have the Template, you need to integrate them into your MediaWiki instance. Simply go to your Import page – http://your_wiki/wiki/index.php/Special:Import – select the file and then hit ‘Upload file’. NOTE: see update at the bottom of the page before doing this.
  5. With the Templates and styles added you should be able to now add a simple infobox. Pick a page and add something like this to the top:{{Infobox
    |title = Infobox Title
    |header1 = Infobox Header
    |label2 = Created by
    |data2 = David
    |label3 = External reference
    |data3 = [https://trog.qgl.org trog.qgl.org]
    }}

The full infobox Template docs are available here – there’s a lot of stuff in there, but if you just want a really basic infobox then this is the simplest way I found to get them working.

I tested this on two separate MediaWiki installs – one running v1.12.1 and one on v1.15.1 – and it worked on both of them, but as always YMMV.

Update 2013-07-27

As many people have noticed, the guide no longer works. Thanks to commenters jh and chojin, it looks like you also need to do the following:

  • Install the Scribunto extension and add it to your LocalSettings.php as usual. It looks like this extension is now required for the InfoBox templates (in fact, it looks like it replaces ParserFunctions entirely, but I’m still testing that).
  • The XML file that is output in step 3 appears to erroneously (?) use text/plain as the format type. If you edit this XML file in your text editor and replace all incidents of ‘text/plain’ with ‘CONTENT_FORMAT_TEXT’ (I only found two), the import will be successful and the infobox tags looks like they work.

If someone else can confirm this for me as a working solution I’ll revise the original post so it takes these steps into account.

96 thoughts on “Setting Up Infobox Templates in MediaWiki”

  1. Thanks for this. Very useful. I did find when I tried to do the import of the xml into my wiki it failed with the error message

    .

    Solution was to add $wgDBmysql5 = false; to LocalSettings.php.

  2. awesome write-up!

    thank you so much!! those other howto-writers really should take a leaf out of your book!

  5. Thank you very much you helped me a lot. THANK YOU.

    I BOOKMARKED YOUR SITE INDEED!!

    CHEERS!!

  7. This was very helpful when I used it a few months back. Thank you a million times over.

    My only additional question is this dumped a lot of pages in my wiki it there a list of which ones I can safely delete? It’s clogging up my “wanted pages” and “wanted categories” lists.

  11. Just ran through this with 1.20. Worked great . Only modifications I made were that it’s not necessary to install ParserFunctions, it’s already bundled as of 1.18, so it just needed to be enabled. I also just copied over the sections in Common.css that contained the infobox data. So far it’s working great. Thanks so much for distilling this down!

  13. I see the same error as “infobox”, for MediaWiki v1.21.1 where the page shows {{#invoke:Infobox|infobox}} instead of the infobox template.

    Turns out the import step failed… at the bottom of the import page, it says:

    Import failed: No handler for model ‘Scribunto” registered in $wgContentHandlers

    It may be related to this bug: https://bugzilla.wikimedia.org/show_bug.cgi?id=45750

  14. I’ll try and update to a new version of MediaWiki and see if I can find a workaround – it’s been a while since I set up a new MediaWiki!

  15. I got it to work for MediaWiki v1.21.1, by importing two templates:

    Template:Info/old
    Template:Main_other

    instead of Template:Info.

    The resultant markup is a bit strange through, since all the content is placed in a and tag.

  16. Sorry, typo in my comment above:

    Template:Infobox/old
    Template:Main_other

    instead of Template:Infobox

    And the content is placed in a DL and DD tag.

  17. I also got the

    {{#invoke:Infobox|infobox}}

    error and missed the error while uploading the template. I installed this extension:

    http://www.mediawiki.org/wiki/Extension:Scribunto

    and then re-uploaded the template and now it seems to be working.

    Thanks, trog, for putting this together. I thought that adding infoboxes would be simple but was starting to get very frustrated while searching and failing to find such a simple guild as this.

  18. I’m getting this error: “Fatal exception of type ScribuntoException”

    I am using MediaWiki Version 1.21.1. Does anyone have any suggestions?

  20. Yes, trog. Thank you for your response. I was getting the {{#invoke:Infobox|infobox}} error until I followed those steps. I can assume that it is at least one step closer to working now, though.

  21. Hello trog,

    I have tried installing the infobox template following your howto but I get the following error when importing:

    Import failed: Format text/plain is not supported for content model Scribunto

    Any idea?

    it is a clean installation.

  22. Sorry man I haven’t had time to look at this problem (that several others have reported)!

    Have you installed the Scribunto extension as suggested by JH?

    I’ll hopefully have a chance to check it out on the weekend and will see if I can figure it out.

  23. I’ve been trying for two days to get it to work on a freebsd box and its still not working so any help would be appreciated.

  24. To fix Import failed: Format text/plain is not supported for content model Scribunto
    I found you have to replace all occurrences of “text/plain” in the import file into “CONTENT_FORMAT_TEXT”

  25. The one thing that I would mention, I haven’t seen a binary package for Freebsd and maybe that’s part of my problem as well. I have installed the Scribunto extension, and added the appropriate lines to the Localsettings.php to reference the engine but now I get a “Script Error” that’s displayed on the screen, when I click on it I get the following error message:

    “Lua error: Internal error: Error reading from pipe.”

  26. Trog,
    If you would like access to a machine to test with, I can give you access to a freebsd box, just drop me an email.

  27. Trog, first I’d like to say thanks so much for having a simple-to-follow guide for infoboxes. I really wish they’d make things a lot clearer on the mediawiki website.

    Second, I’m having the exact same issue as Jano:

    Clean install. Scribunto IS installed and is showing in the installed extensions list, and I’m getting the following error message.

    Import failed: Format text/plain is not supported for content model Scribunto

    I’m going to play around with it and see if I can figure out what the issue is, but honestly, I’m a layman myself.

  28. jc / D.W, have you guys tried the solution outlined by chojin – replace all occurrences of “text/plain” in the import file into “CONTENT_FORMAT_TEXT”?

  29. Feel free to delete my previous post. :) The solution was given; my browser just wasn’t updating with the recent posts.

    Thanks a million for the awesome guide, Trog!

  30. I’ve updated the OP with the steps provided by others (thanks guys); when I follow that it seems to work fine.

    If people can try these steps and see if that works that’d be great:

    – Install the Scribunto extension and add it to your LocalSettings.php as usual. It looks like this extension is now required for the InfoBox templates (in fact, it looks like it replaces ParserFunctions entirely, but I’m still testing that).
    – The XML file that is output in step 3 appears to erroneously (?) use text/plain as the format type. If you edit this XML file in your text editor and replace all incidents of ‘text/plain’ with ‘CONTENT_FORMAT_TEXT’ (I only found two), the import will be successful and the infobox tags looks like they work.

  31. I’m still getting an error, “Script Error” which when I click on it it shows a box with the following:

    Script error: No such module.

    I have the Module:Infobox installed so I’m not sure what else could be missing.

  32. Ok, I went ahead and re-uploaded the files and that seems to have taken care of the issue, although I did have to change the path and point it to a port of lua that I installed (freebsd).

    One thing though, I don’t see the lines around the boxes on my Infobox page like I do here:

    https://en.wikipedia.org/wiki/Module:Infobox

    so I’m not sure its working…..

    I’m just not getting script errors anymore.

  33. D.W. Palme: I had the same problem in my testing and realised I’d forgotten to do Step 2 in my list – copying over the CSS. Have you definitely done that part?

  34. Trog, firstly thank you for your clear and concise method of getting infoboxes to work on mediawiki sites. Your page is by far the most helpful I have found.

    I’ve done all the steps, including those described in the 27th June update. Scribuntu is installed on my Wiki and I’ve successfully imported ‘Template:Infobox’ from Wikipedia.

    However when I try to create an infobox on the editing section of any page, nothing is displayed on the page.

    A possible reason could be that I created an empty page called: ‘Template:Infobox’ on my wiki before I found your article. Could it be interfering with the ‘Template:Infobox” file I imported from wikipedia? I’ve subsequently deleted my ‘Template:Infobox’ page and re-imported the ‘Template:Infobox’ file from wikipedia, but it has made no difference.

    Thank you for any assistance, advice or suggestions.

  35. Werner: I am not sure. I would guess that the creation of the empty page may have interfered with it – it’s possible that the subsequent import might have ended up creating a different template name because ‘infobox’ was taken, or something similarly weird like that. If you visit the /index.php/Template:Infobox page on your Wiki, does anything show up?

  36. Yes I have it copied over, I have one page that the alignment is like totally malformed, big time and its still got some errors it looks like with the script.

  37. Hey, i got an error if i try to import the wikipedia site. Warning: proc_open() has been disabled for security reasons.

    Can i fix that?

  38. Thank you for your response, I apologize for my delayed reply.

    The ‘template:Infobox’ page on my wiki is currently empty. I have once again tried re-importing the ‘Template:Infobox’ from Wikipedia, however it now fails. After clicking ‘upload’ on the: ‘…/w/index.php?title=Special:Import&action=submit’ page it merely shows the same URL and a empty page.

    Having the infobox functionality on my wiki is important for allowing other users to create and update pages in certain categories . If necessary I am prepared to reinstall the mediawiki software and copy across the necessary pages.

    Thank you for any suggestions.

  41. The supplementary instructions about Scribunto, specifically replacing text/plain with CONTENT_FORMAT_TEXT, worked for one of my imports, but not the other. I was able to successfully import a set of templates exported from Template:Cite web, but not able to import the full set of templates from Template:About.

    By turning the Scribunto extension on and off I was able to import enough to where my site is functional, but there may be a little more going on here than you’ve uncovered. The specific error I get is:

    Import failed: Expected tag, got

  42. I am having the same issue as Dennis and Werner..
    seems to be related to the Template:Infobox template with the code {{#invoke:Infobox|infobox}}.
    When this is added, Scrinbunto comes back with a Fatal exception of type ScribuntoException.
    Been digging around the net and cannot seem to find a solution.

    Any ideas Trog? And thank you for this infobox step by step.

  43. Thanks David, Your instructions really helped.
    After getting various Import failed: Lua error: … errors the following worked for me in importing the infobox template:
    1. chmod/Change permissions to 755 for the file extensions/Scribunto/engines/LuaStandalone/binaries/lua5_1_5_linux_64_generic/lua
    2. Remove //$wgScribuntoDefaultEngine = 'luastandalone'; from LocalSettings.php

  44. Gary,
    thank you, that fixed my Fatal Exception error on the info box template..
    Thank you..

  45. Hi,

    Following the guide + its recent update, I run into a problem. I wish to point out that while replacing “text/plain” in the template, I find 3 strings to replace, not 2 like mentioned in the update.

    Scribunto in installed, the ParserFunctions as well. The template import works fine as well.

    When I copy/paste the {{Infobox …. }} on a page, I get the following error message: “Lua error: Internal error: The interpreter exited with status 1.”

    I could paste the backtrace here, but it would be a bit big.

    Yes, all lua extension files have 755 permissions set.

    No clue what the cause of it is. The tutorial seemed so clear and easy, yet I can’t manage to make the infobox work.

  46. Hi all,
    I’m having the same problems as listed above:
    Lua error: Internal error: The interpreter exited with status 126.
    According to the specific exit code:
    126 Command invoked cannot execute /dev/null Permission problem or command is not an executable

    The templates installed perfectly once I’d accounted for the extra changes at the bottom of the write up. I’m betting there’s something wrong with the extension.

    I have tried the changes Gary suggested as well with no luck.

    Thanks in advance for any assistance.

  47. Thanks for putting the update at the bottom of the page. I got through all the steps only to realize this doesn’t work anymore.

    Thanks for nothing

  48. Apologies, I was waiting for feedback from other people to confirm that the new steps worked. It never occurred to me that people wouldn’t read the whole post if they had problems so I thought having it at the bottom was fine, but I guess some people just run through the steps and panic when things don’t work as expected and jump straight to the comments :)

    I have integrated the update steps into the main post; this still seems to work for me.

    I wonder if some platforms handle the import differently due to different system libraries or something.

    Oli, do you have any more info about what OS you’re running on?

  49. Finally managed to get my host to inform me that .sh and .exe files are not allowed to run on their system which is the root of my issue. I’m certain at this point that everything is installed correctly and that my host, iPage has simply disabled the functions necessary.

    Thank you for the fantastic walk through.

  50. Thank you for the only tutorial that gives up hope in here, even though it again seems to have run into a wall. I am sure that the collective wisdom will help us solve it again.

    I have Mediawiki 1.19 installed on a 32 bit Ubuntu machine and I tried the steps suggested by you, including those suggested later. However, when I create the sample info box, I get the error: “Scribunto needs MediaWiki 1.20 or later (Preprocessor::SUPPORTS_INDEX_OFFSET)”. I am sure I selected 1.19 when downloading the Scribunto extension. I tried the other suggestions like those of Gary, but they did not work for me too.

    In case it helps, this is the backtrace I get:
    Backtrace:

    #0 [internal function]: ScribuntoHooks::invokeHook(Object(Parser), Object(PPTemplateFrame_DOM), Array)
    #1 /etc/mediawiki/includes/parser/Parser.php(3197): call_user_func_array(‘ScribuntoHooks:…’, Array)
    #2 /etc/mediawiki/includes/parser/Preprocessor_DOM.php(1043): Parser->braceSubstitution(Array, Object(PPTemplateFrame_DOM))
    #3 /etc/mediawiki/includes/parser/Parser.php(3357): PPFrame_DOM->expand(Object(PPNode_DOM))
    #4 /etc/mediawiki/includes/parser/Preprocessor_DOM.php(1043): Parser->braceSubstitution(Array, Object(PPFrame_DOM))
    #5 /etc/mediawiki/includes/parser/Parser.php(2986): PPFrame_DOM->expand(Object(PPNode_DOM), 0)
    #6 /etc/mediawiki/includes/parser/Parser.php(1099): Parser->replaceVariables(‘{{Infobox?|name…’)
    #7 /etc/mediawiki/includes/parser/Parser.php(345): Parser->internalParse(‘{{Infobox?|name…’)
    #8 /etc/mediawiki/includes/WikiPage.php(1522): Parser->parse(‘{{Infobox?|name…’, Object(Title), Object(ParserOptions), true, true, NULL)
    #9 /etc/mediawiki/includes/WikiPage.php(1290): WikiPage->prepareTextForEdit(‘{{Infobox?|name…’, NULL, Object(User))
    #10 [internal function]: WikiPage->doEdit(‘{{Infobox?|name…’, ”, 98)
    #11 /etc/mediawiki/includes/Article.php(1783): call_user_func_array(Array, Array)
    #12 /etc/mediawiki/includes/EditPage.php(1435): Article->__call(‘doEdit’, Array)
    #13 /etc/mediawiki/includes/EditPage.php(1435): Article->doEdit(‘{{Infobox?|name…’, ”, 98)
    #14 /etc/mediawiki/includes/EditPage.php(960): EditPage->internalAttemptSave(Array, false)
    #15 /etc/mediawiki/includes/EditPage.php(357): EditPage->attemptSave()
    #16 /etc/mediawiki/includes/actions/EditAction.php(51): EditPage->edit()
    #17 /etc/mediawiki/includes/actions/EditAction.php(71): EditAction->show()
    #18 /etc/mediawiki/includes/Wiki.php(484): SubmitAction->show()
    #19 /etc/mediawiki/includes/Wiki.php(278): MediaWiki->performAction(Object(Article))
    #20 /etc/mediawiki/includes/Wiki.php(593): MediaWiki->performRequest()
    #21 /etc/mediawiki/includes/Wiki.php(503): MediaWiki->main()
    #22 /etc/mediawiki/index.php(58): MediaWiki->run()
    #23 {main}

    Thanks again for your help.
    Cheers!

Leave a Reply

Your email address will not be published. Required fields are marked *


The reCAPTCHA verification period has expired. Please reload the page.